Link Search Menu Expand Document
docs @ O|D
This page is a DRAFT.

Limiter Unit

Soft or hard clip a signal.
Limiter
pre

Overview

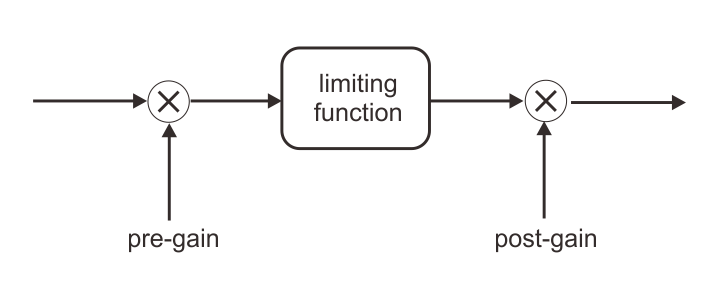
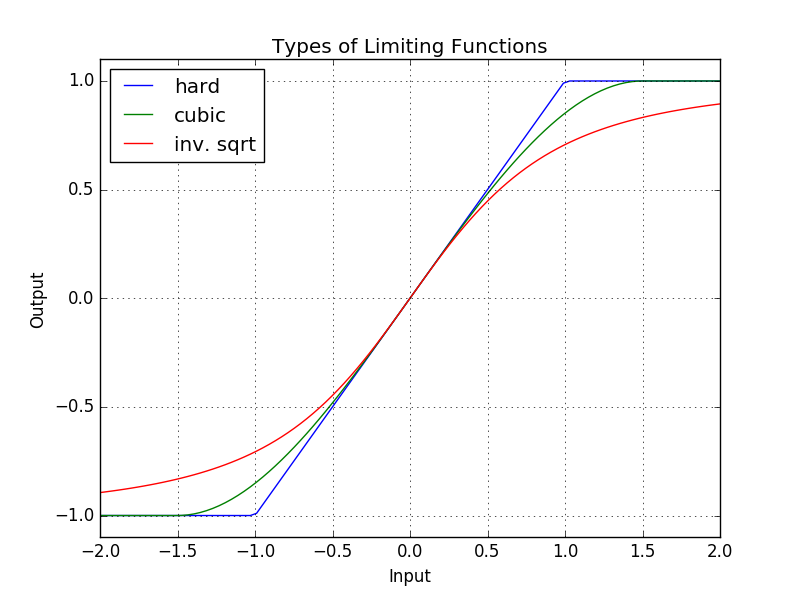
This unit implements 3 limiting algorithms: hard, cubic and inverse square root. The hard algorithm adds the most (odd) harmonics while the inverse square root adds the least. Furthermore, there are separate pre-gain and post-gain stages so that you can dial in the exact amount of non-linearity that you desire in the final output.

limiter.png
tip

Inserting a Fixed HPF (high pass filter) unit right before a Limiter unit is a great way to maximize dynamic range. The HPF will remove any (inaudible) DC offset which if left alone would reduce the headroom available for higher frequencies.
tip

The opposite of the above tip is to place an Offset unit before a Limiter to cause pre-mature clipping (under CV control) on purpose as a kind of sound design technique.
tip

Whether you use a Limiter or not, signals are always passed through a hard limiter right before being sent out to the DAC (i.e. OUT1-4).

Some applications are:

  • Gain-staging
  • Memory-less saturation
  • Soft-limiting
  • Adding odd harmonics to sinusoidal waveforms (i.e. squaring off or flattening peaks)
  • Sound design
  • Shaping modulation signals (envelopes and LFOs)
  • Taming feedback loops

Parameters

pre

Simple Fader
pre-limiting gain

This gain multiplies the signal before the non-linearity affects it.

type

Option

Here you choose from one of the 3 available limiting functions:

limiting-functions.png

Hard Limiting

Any signal above 1 is clipped to 1 and any signal below -1 is clipped to -1.

\[\mbox{CLIP}(x,m) = \begin{cases} -m, & x < -m \\ x, & -m \le x \le m \\ m, & x > m \\ \end{cases}\] \[\mbox{HARD}(x) = \mbox{CLIP}(x,1)\]

Cubic Limiting

The input range between -1.5 and 1.5 is mapped to a cubic spline and clipped outside that range in such a way that the first and second derivatives are continuous everywhere (i.e. C2 smoothness).

\[\mbox{CUBIC}(x) = \mbox{CLIP}(x,1.5) - \frac{\mbox{CLIP}(x,1.5)^3}{6.75}\]

Inverse Square Root Limiting

The output asymptotically approaches 1 from below and -1 from above. This limiting function is the softest of the three.

\[\mbox{INVSQRT}(x) = \frac{x}{\sqrt{x^2 + 1}}\]

post

Simple Fader
post-limiting gain

This gain multiplies the signal after the non-linearity affects it.